It is sometimes desirable to have circuits capable of selectively filtering one frequency or range of frequencies out of a mix of different frequencies in a circuit. A circuit designed to perform this frequency selection is called a filter circuit, or simply a filter.
A common need for filter circuits is in high-performance stereo systems, where certain ranges of audio frequencies need to be amplified or suppressed for best sound quality and power efficiency.
You may be familiar with equalizers, which allow the amplitudes of several frequency ranges to be adjusted to suit the listener’s taste and acoustic properties of the listening area.
You may also be familiar with crossover networks, which block certain ranges of frequencies from reaching speakers.
A tweeter (high-frequency speaker) is inefficient at reproducing low-frequency signals such as drum beats, so a crossover circuit is connected between the tweeter and the stereo’s output terminals to block low-frequency signals, only passing high-frequency signals to the speaker’s connection terminals.
This gives better audio system efficiency and thus better performance. Both equalizers and crossover networks are examples of filters, designed to accomplish filtering of certain frequencies.
Another practical application of filter circuits is in the “conditioning” of non-sinusoidal voltage waveforms in power circuits.
Some electronic devices are sensitive to the presence of harmonics in the power supply voltage, and so require power conditioning for proper operation.
If a distorted sine-wave voltage behaves like a series of harmonic waveforms added to the fundamental frequency, then it should be possible to construct a filter circuit that only allows the fundamental waveform frequency to pass through, blocking all (higher-frequency) harmonics.
We will be studying the design of several elementary filter circuits in this lesson. To reduce the load of math on the reader, I will make extensive use of SPICE as an analysis tool, displaying Bode plots (amplitude versus frequency) for the various kinds of filters.
Bear in mind, though, that these circuits can be analyzed over several points of frequency by repeated series-parallel analysis, much like the previous example with two sources (60 and 90 Hz), if the student is willing to invest a lot of time working and re-working circuit calculations for each frequency.
A filter allows you to remove unwanted frequencies and also allows you to boost certain frequencies. Which frequencies are removed and which frequencies are left depends on the type of filter you use.
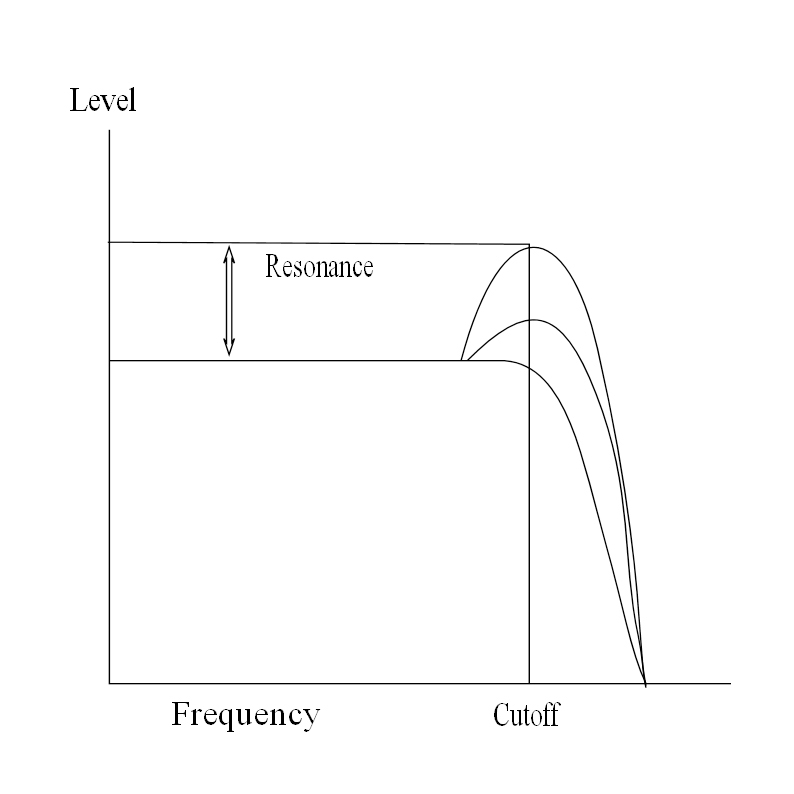
Cut-off frequency
This is the point (frequency) at which the filter begins to filter (block or cut out). The filter will lower the volume of the frequencies above or below the cut-off frequency depending on the type of filter used.
This ‘lowering of the volume of the frequencies,’ is called Attenuation. In the case of a low pass filter, the frequencies above the cut off are attenuated. In the case of a high pass filter, the frequencies below the cut off are attenuated. Put simply: in the case of a low pass filter, we are trying to block the (higher) frequencies above a certain point and allow the lower frequencies through. In the case of a high pass filter, the opposite is true. We try to cut out or block frequencies below a certain point and allow the higher frequencies through.
Analogues use circuitry and for that reason alone, it takes time for the filter to attenuate frequencies, in proportion to the distance from the cut-off point. Today’s technology allows for instant cut-off as the filter attenuation is determined by algorithms as opposed to circuits. That is why the filters of an Arp or Oscar etc, are so much more expressive and warm as they rely completely on the resistors and capacitors to first warm up, then to work but in a gradual mode(gradual meaning sloped or curved as opposed to instant). Depending on how well a filter attenuates or the way it attenuates gives us an idea of the type of sound we will achieve with an analogue filter.
Slope/Gradient
The speed at which the filter attenuates is called the slope or gradient. Another point to raise now is that you will often see values on the filter knobs on analogue synthesizers that have 12 dB or 24 dB per octave. That basically means that each time the frequency doubles, the filter attenuates by 12 dB or 24 dB everything at that frequency. These are also known as 2 pole or 4 pole filters, each pole represents 6 dB of attenuation. This is how analogue circuits were built, the number of circuits being used by the filter to perform the task at hand.
Resonance
Most synthesizer manufacturers, and in the case of most analogue synthesizers, the term resonance is used most commonly. Other manufacturers of synthesizers, or software synthesizers, might call it emphasis or Q.